Praktische Betrachtungen zu hohlen Stämmen
Einleitend ein paar Erläuterungen, wieso der
Stammaußendurchmesser so viel wichtiger als die Innenfäule ist.
Ein Grund
dafür lässt sich schon anhand von Bild 2 und 3 leicht nachvollziehen.
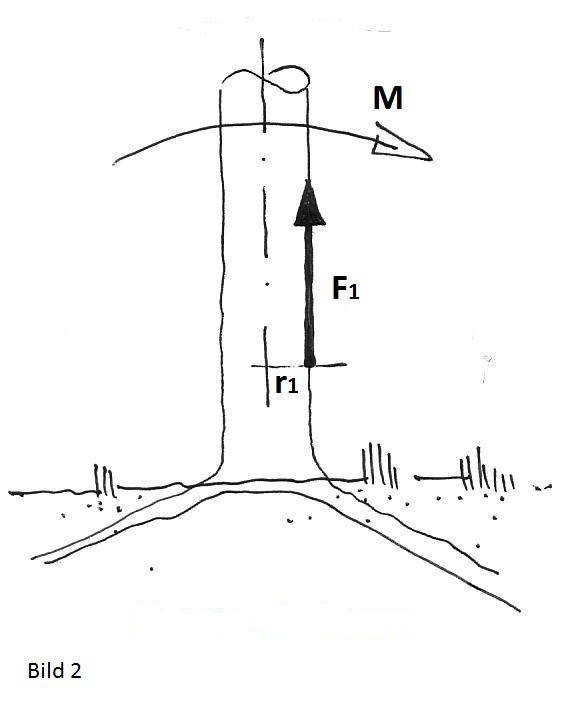
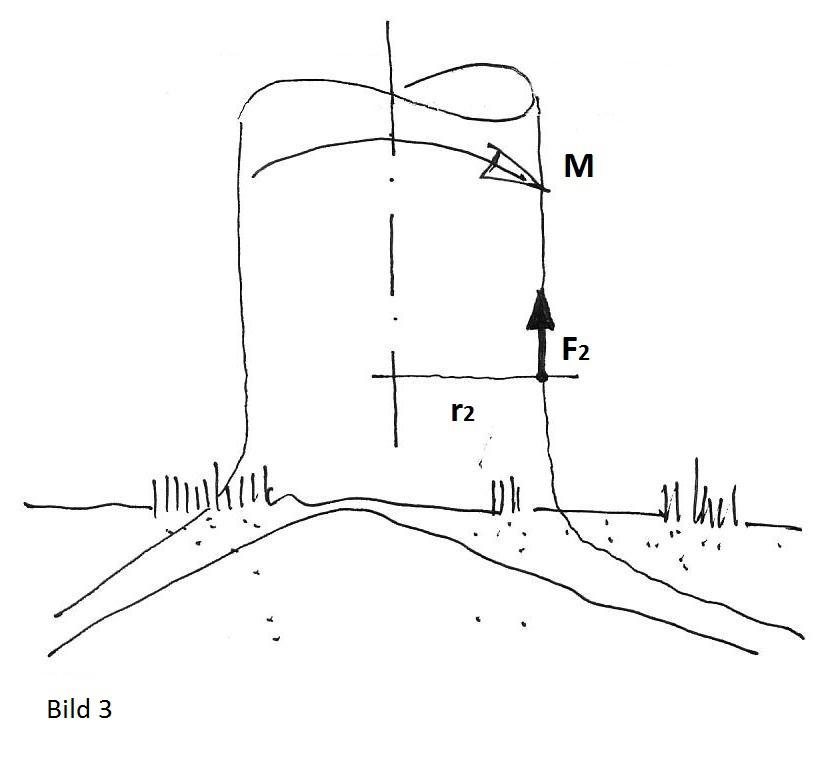
F1 x r1 = M = F2 x r2
Bei gleicher Belastung (M) des Baumstammes gibt es eine starre
Relation zwischen Radius (r) und Belastung der Randfaser (F). Nimmt der Radius
zu, so wird die Last der Randfaser kleiner. Bei gleicher (Wind-) Last hat der
linke Baum eine mehrfach höhere Spannung in seinen Randfasern.
Mehr
Stammdicke macht die Bäume sicherer, weil die Last im Stamm, die die Randfaser
abtragen muss, deutlich kleiner ist. Großer Radius ergibt kleine Kräfte.
Ein weiterer Grund ist die Lastverteilung im Stamm:
Im
Stamminneren herrscht keine Zug- und Druckspannung. Nach außen nehmen diese aber
linear zu und erreichen an der Randfaser ihr Maximum. Dabei „nimmt“ jede Faser
die jeweilige Nachbarfaser mit. Das geht umso länger, je geringer der
Lastunterschied zwischen den Fasern ist.
Es sind hauptsächlich die äußersten
Fasern an der Kraftableitung beteiligt. Der Einfluss des Stamminneren auf die
Bruchsicherheit ist, auch bei Vollholzigkeit, sehr gering.
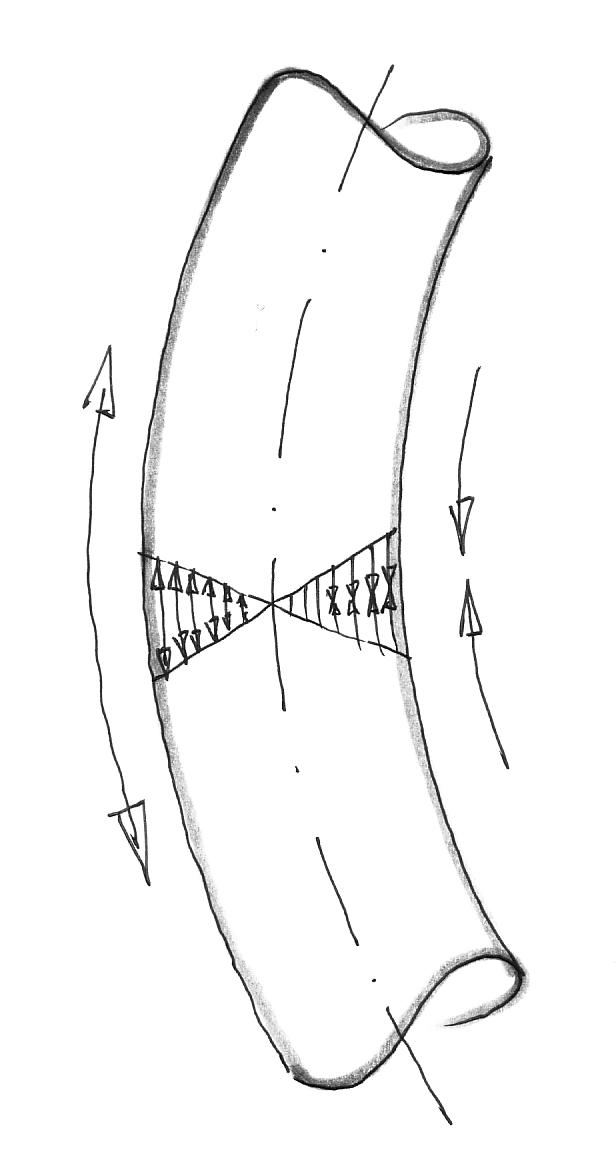

Bei kleinerer Last sind die Spannungsunterschiede zwischen den einzelnen Fasern geringer und mehr Faserbündel beteiligen sich an der Lastabtragung.
Den oben angeführten Fakten folgt auch dieses Diagramm das wohl allen bekannt ist. Es ist unstrittig und wird auch von VTA verwendet und als richtig anerkannt (Abb. 5, VTA).
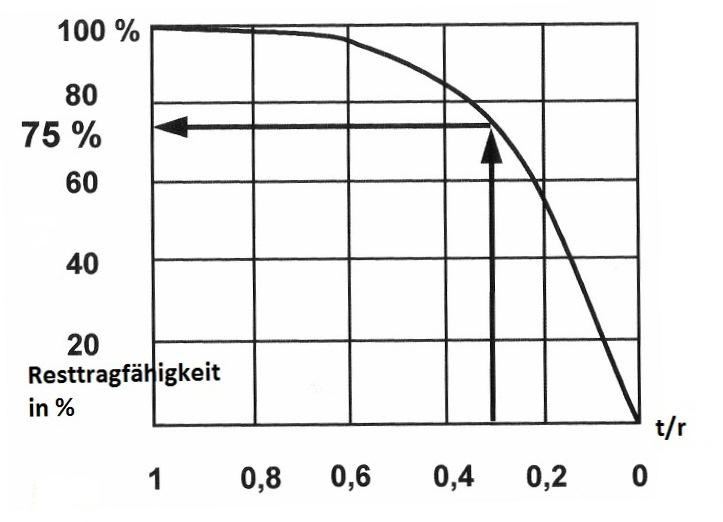
Quelle: Diagramm zur Resttragfähigkeit hohler Baumstämme, Prpf. Dr. Claus Matteck
Daraus lässt sich ableiten, dass eine Ausmorschung von 70 % eine
Reduktion der Tragfähigkeit von nur 25% verursacht. Diesem Diagramm liegt die
Berechnung des Widerstandmomentes zugrunde. Das Widerstandsmoment (W) ist ein
Maß dafür, wie bruchfest ein Querschnitt unter Berücksichtigung seiner
geometrischen Form ist.
W beschreibt in unserem Fall, wie stabil ein Kreis,
oder ein Kreisring gegen Bruch ist.
Mit der Formel σ = M/W wird der Widerstand der geometrische Form mit der Last verknüpft und man erhält die Spannung der Randfaser bei Biegung. M ist das Biegemoment, dass durch die Windlast in den Stamm eingeleitet wird, W das Widerstandsmoment das dem Biegemoment entgegen wirkt. Aus diesen Kräften leitet sich die Spannung σ der Randfaser ab.
Für den Kreis:
D ist der
Stammaußendurchmesser
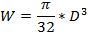
Für den Kreisring:
D ist der Stammaußendurchmesser
d
Durchmesser der
Höhlung
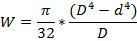

Der Stamm mit dem Durchmesser 50 cm wird als Referenzstamm gewählt, seine Sicherheit wird mit 1 festgelegt.
Morscht dieser Stamm zu 70 % aus, so reduziert sich seine Bruchsicherheit auf 0,76 %, gerundet 0,75 %. Einem beträchtlichen Substanzverlust steht ein geringer Verlust an Bruchfestigkeit gegenüber. Die Höhlung scheint keinen großen Einfluss auf das Widerstandsmoment zu haben. Dieser Zusammenhang wird auch von VTA (sie Diagramm oben) anerkannt.
Verdoppeln wir den Außendurchmesser auf 100 cm, erhöht sich die Bruchfestigkeit auf das 8-Fache. Das ist viel! Man hätte das Doppelte, oder vielleicht das 4-Fache erwartet, aber der Außendurchmesser geht mit D³ in die Formel ein.
Der Außendurchmesser ist der wesentlichste Einflussfaktor auf das Widerstandsmoment!
Damit ist der Außendurchmesser auch der wesentlichste Einfluss auf
die Spannung der Randfaser und somit auch die Bruchsicherheit der Baumstämme.
Morscht der 100 cm dicke Stamm innen 70 % aus, erreicht man wieder das
VTA-Versagenskriterium. Nach VTA erwarten wir also 0,75 % Bruchsicherheit, wie
beim ersten Stamm. Nach VTA sind alle Stämme mit 70% Ausmorschung unsicher und
vielleicht merkt man an diesem Punkt, dass dieses, nur durch eine Zahl
definierte, Kriterium nicht einmal theoretisch stimmen kann.
Ein 100 cm
Stamm, 70% ausgemorscht, ist 6-mal so bruchsicher wie ein Stamm mit 50 cm
Durchmesser ohne Ausmorschung, aber nach VTA versagt er gerade.
In der Natur lassen sich durchaus Bäume mit sehr ähnlichen Baumkronen und Baumhöhen finden. Der eine hat 50 cm Stammdurchmesser, der andere 100 cm. Jetzt nehmen wir an, der 100 cm Stamm ist zu 70 % ausgemorscht. Das ist dann ein Baumveteran, mit historischem Wert, ev. standortprägend. Er hat Spechtlöcher, Faulstellen, Totholz, usw. Somit ist er ein biologisch und historisch wertvoller Baum.
Nach den gültigen Formeln der Technik ist der Baum mit
ausgemorschtem Stamm sechsmal so sicher wie der Baum mit vollholzigem 50 cm
Stamm.
Nach t/r = 0,3 ist der 100 cm Stamm unsicher, der 50 cm Stamm
sicher.
Es ist nicht zulässig, dass zwei Baumbegutachtungsverfahren zu derart unterschiedlichen Ergebnissen kommen. Das darf die „Scientific Community“ nicht zulassen. Wir Gutachter müssen jetzt rasch zu einer Einigung kommen und jeder ist aufgerufen dazu beizutragen! 30 Jahre sind genug.
Wo liegt der Fehler?
Der Fehler liegt
darin, dass VTA behauptet ab 70% Ausmorschung ändere sich das Versagenskriterium
der Stämme von Faserstauchen zu Rissen, womit diese Formel vom
Wiederstandsmoment ab 70% Ausmorschung nicht mehr gültig wäre. Dafür konnte aber
von VTA-Seite noch nie ein plausibler Nachweis geführt werden. Es sind
Behauptungen die sich in der Natur nicht wiederfinden. Was in der einzigen
Bestätigung, die es geben soll, der weltweiten Feldstudie, untersucht und
gemessen wurde ist unbekannt und nicht nachprüfbar. Diese Studie darf erst
Berücksichtigung finden, wenn eine kritische Betrachtung und Analyse ermöglicht
wurde.
Die Studien von Wagener, sowie Smiley u. Fraedrich, die gerne von Mattheck zitiert werden, behandeln Waldbäume und wurden für den Forst durchgeführt. Waldbäume stehen im Bestand und entwickeln verstärktes Höhenwachstum bei Vernachlässigung der Stammdicken. Sie sind auch ohne Höhlung schon kritisch dünn, da sie zu geringe Außendurchmesser haben. Es ist sehr gut möglich, dass die meisten dieser Bäume bei 25% Festigkeitsverlust brechen können.
Es ist aber eine Missinterpretation dieser Studien, wenn die Bruchsicherheitsreserven von Waldbäumen auf Stadt- und Solitärbäume übertragen werden. Stadt- und Solitärbäume haben deutlich dickere Stämme und dürfen daher deutlich mehr ausmorschen als Waldbäume.
Wiederum zeigt sich, dass ein einziges Kriterium den unterschiedlichen Bäumen niemals gerecht werden kann.
Wir haben eine wissenschaftliche Arbeit erstellt, deren Grundlagen und Ergebnisse veröffentlicht wurden. Sie bestätigt die Annahmen von SIA und widerspricht den Thesen von VTA.
© 2017 Sachverständigenbüro Rainer Prosenz. All rights reserved.
